岛屿数量计算中的DFS和BFS的应用

共计 1550 个字符，预计需要花费 4 分钟才能阅读完成。

前言

计算岛屿数量是在由 ’0’ 与 ’1’ 的二维网格中寻找竖直的上下左右被 ’1’ 包围的岛屿数量（如果是多个 ’1’ 连接在一起，则算作一个岛屿），如：

01000
11100
10000
00010

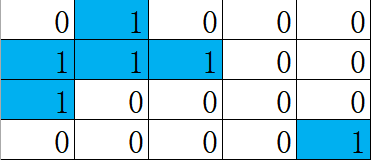
在上述的二维网格中，岛屿数量为 2，图解岛屿的具体分布为：

DFS 方式

对于计算岛屿数量可以采用 DFS 的方式进行解决，由 [0,0] 开始，依次进行目标点的上下左右四个点搜索其值为 ’1’ 的单元，即为(r+1,c) ,(r-1,c)，(r,c+1), (r,c-1), 如遇到非 ’1’ 的则返回，将遇到 ’1’ 的也要进行改变为 ’0’，避免重复搜索，进而导致无限递归循环，Golang 实现：

package main

import "fmt"

func lands(grid [][]byte) int {
    res := 0
    for r, row := range grid {
        for c, v := range row {
            if v == '1' {dfs(grid, r, c)
                res++
            }
        }
    }
    return res
}

func dfs(grid [][]byte, r, c int) {if !(r >= 0 && r < len(grid) && c >= 0 && c < len(grid[0])) {return}
    if grid[r][c] != '1' {return}
    grid[r][c] = '0'
    dfs(grid, r+1, c)
    dfs(grid, r-1, c)
    dfs(grid, r, c+1)
    dfs(grid, r, c-1)
}

func main() {grid := [][]byte{{'0','1','0','0','0'},
        {'1','1','1','0','0'},
        {'1','0','0','0','0'},
        {'0','0','0','0','1'},
    }
    fmt.Printf("岛屿的数量为：%d\n", lands(grid))
}

运行输出为：

岛屿的数量为：2

BFS 方式

使用广度优先搜索，其思路和 DFS 有些类似，不同的是搜索的方式不一样，其区别在于 BFS 是使用一个队列，取出首部的节点 (r,c) 判断是否为未越界并且为 ’1’，若是则将此点的上下左右节点加入队列等待判断，若不是则跳过此节点，如：

package main

import "fmt"

func lands(grid [][]byte) int {
    res := 0
    for r, row := range grid {
        for c, v := range row {
            if v == '1' {bfs(grid, r, c)
                res++
            }
        }
    }
    return res
}

func bfs(grid [][]byte, r, c int) {queue := [][]int{{r, c},
    }
    for len(queue) > 0 {r = queue[0][0]
        c = queue[0][1]
        queue = queue[1:]
        if r >= 0 && r < len(grid) && c >= 0 && c < len(grid[0]) && grid[r][c] == '1' {grid[r][c] = '0'
            queue = append(queue, [][]int{{r + 1, c},
                {r - 1, c},
                {r, c + 1},
                {r, c - 1},
            }...)
        }
    }
}

func main() {grid := [][]byte{{'0', '1', '0', '0', '0'},
        {'1', '1', '1', '0', '0'},
        {'1', '0', '0', '0', '0'},
        {'0', '0', '0', '0', '1'},
    }
    fmt.Printf("岛屿的数量为：%d\n", lands(grid))
}

总结

DFS 和 BFS 都是搜索算法，其主要区别为 DFS 利用递归的方式实现，而 BFS 使用队列的方式实现。归结到现实生活中来解释这两种的算法的规则就如：DFS 中就像一个固执不己的年轻人坠入爱河，不撞南墙不回头。而 BFS 就像是撞了南墙多年后释怀了的年轻人，再往那平静的湖面扔一块石头而周围泛起那一波波涟漪。